




The calculator below evaluates the Lambert function W(x) for the variable x, which is defined to be the solution to the equation:
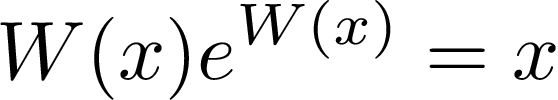
Equivalently, the Lambert function is the inverse of the function:
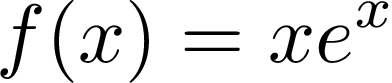
Simply enter a value for x and click “Calculate W(x)” to find the value of the function.
Click here to see how the Lambert function can be used in order to solve the transcendental equation below:
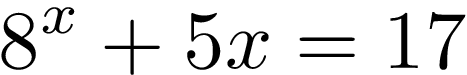
In order to analyze the Lambert function, it is easier to consider its inverse function f(x) as defined above. First, we note that the domain of this inverse function is clearly (-∞,+∞). In order to find its range, we calculate the 1st and 2nd derivatives:
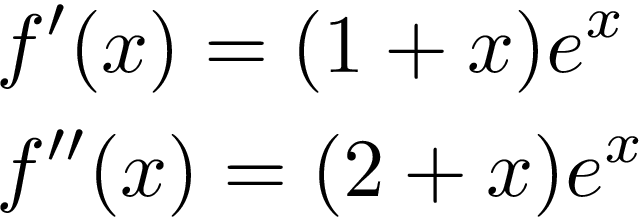
We see that f(x) has an extremum for x=-1:
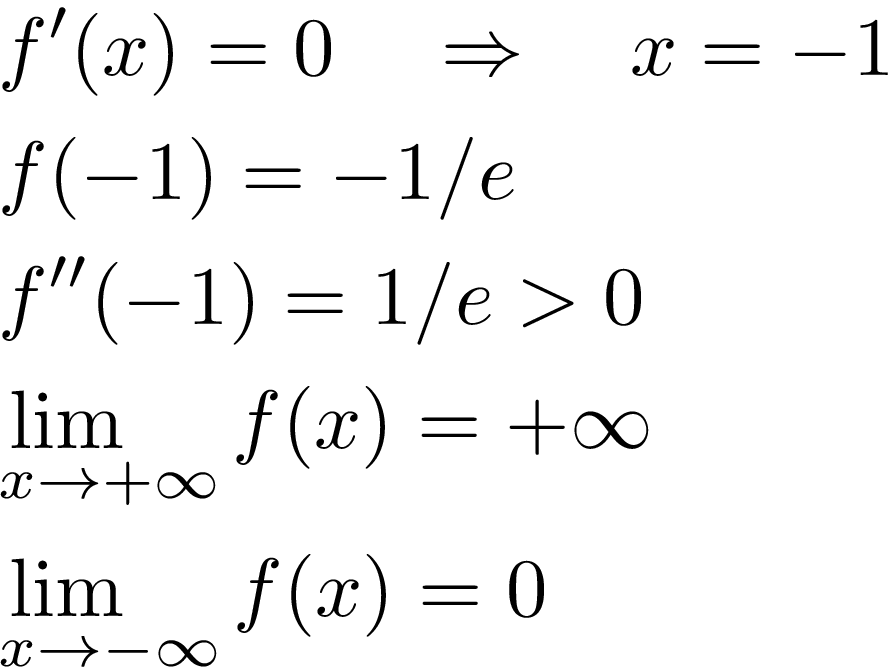
It follows that the extremum is a global minimum with value -1/e and the maximum of the invserse function is +∞. Its range is therefore [-1/e,∞). As a consequence, the domain of the Lambert function is [-1/e,∞) and the range is (-∞,+∞). From the analysis of the inverse function f(x), we conclude that W(x) satisfies the following relations:
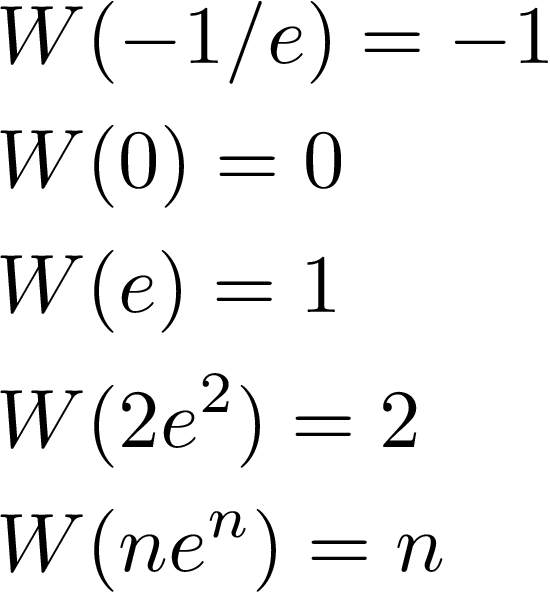
Since the inverse function f(x) has a global minimum, it follows that the Lambert function W(x) has two branches:
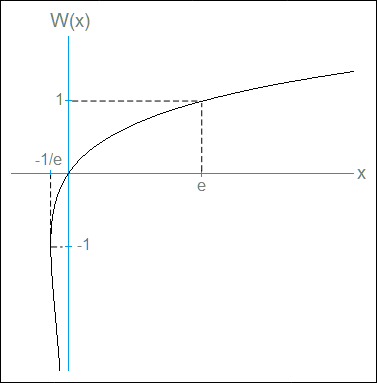
From its definition, it follows that W(x) satisfies the functional relations:
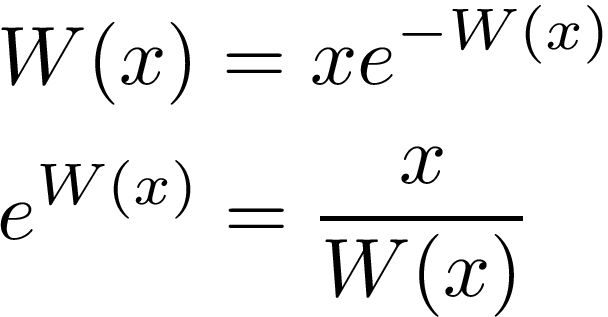
Using implicit differentiation and the above functional relations, we can easily calculate the 1st derivative:
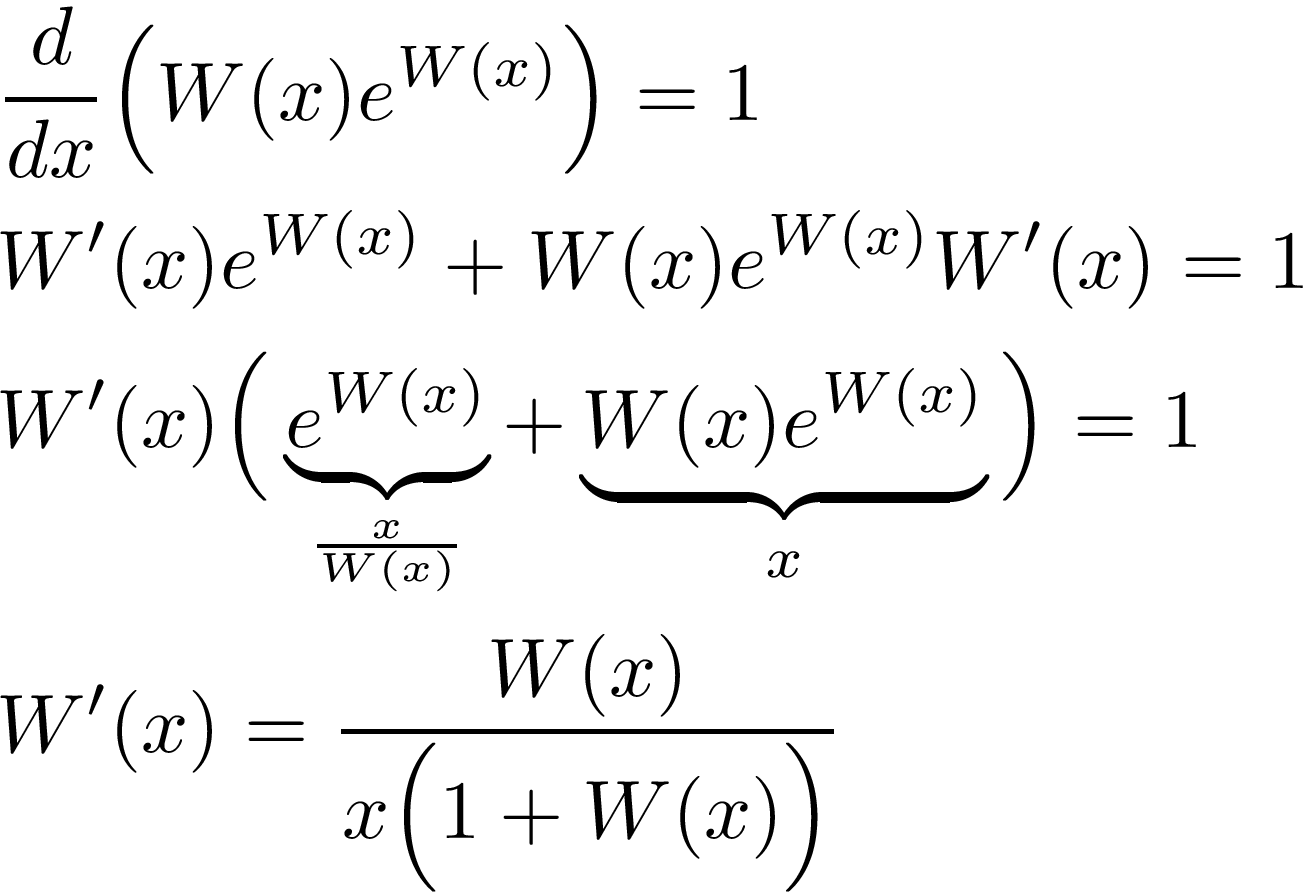
The 2nd derivative can then be obtained as well:
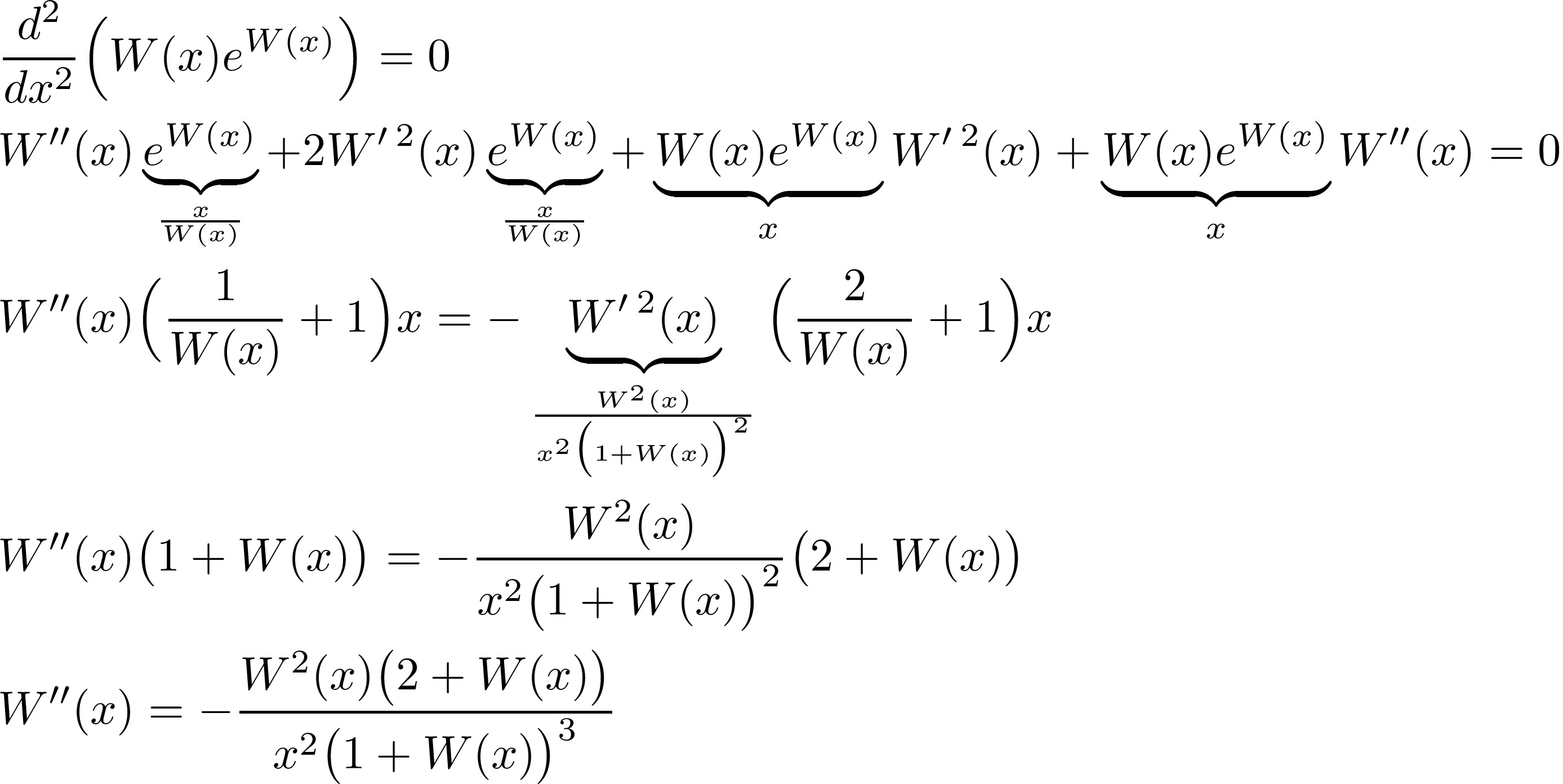
In order to find an antiderivative of W(x), we can start with an integration by parts:
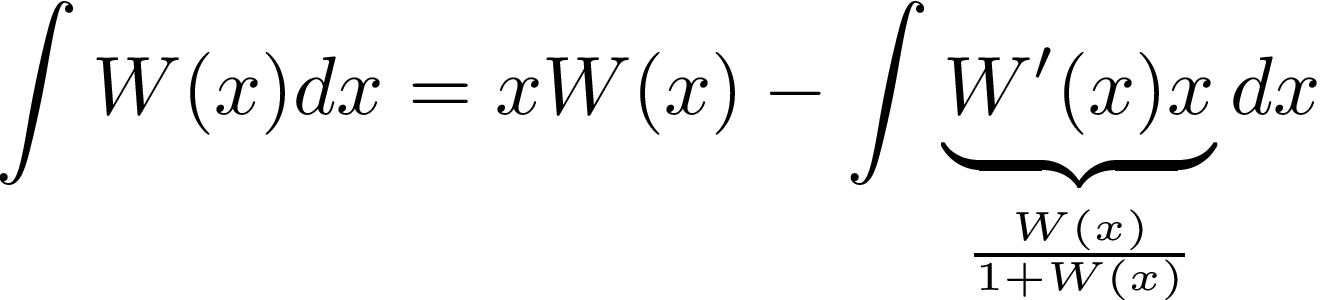
Writing the integrand of the remaining integral as
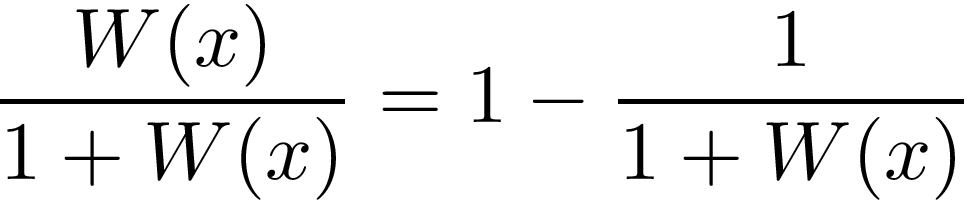
leads to:

Using the expression of the derivative found earlier, we can rewrite the infinitesimal element dx in terms of dW:
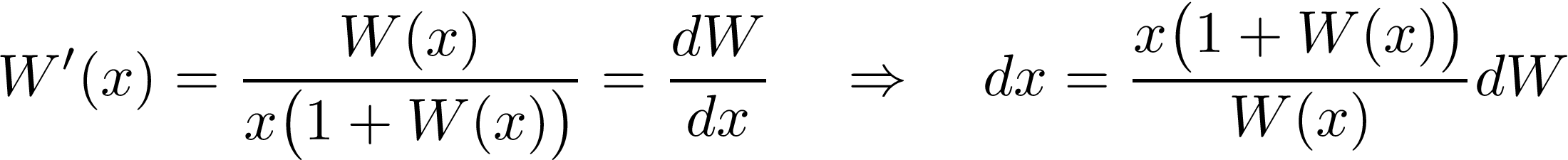
This leads to:
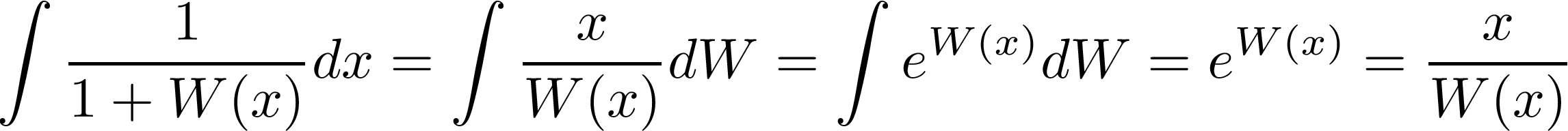
Putting everything together, we have shown that:
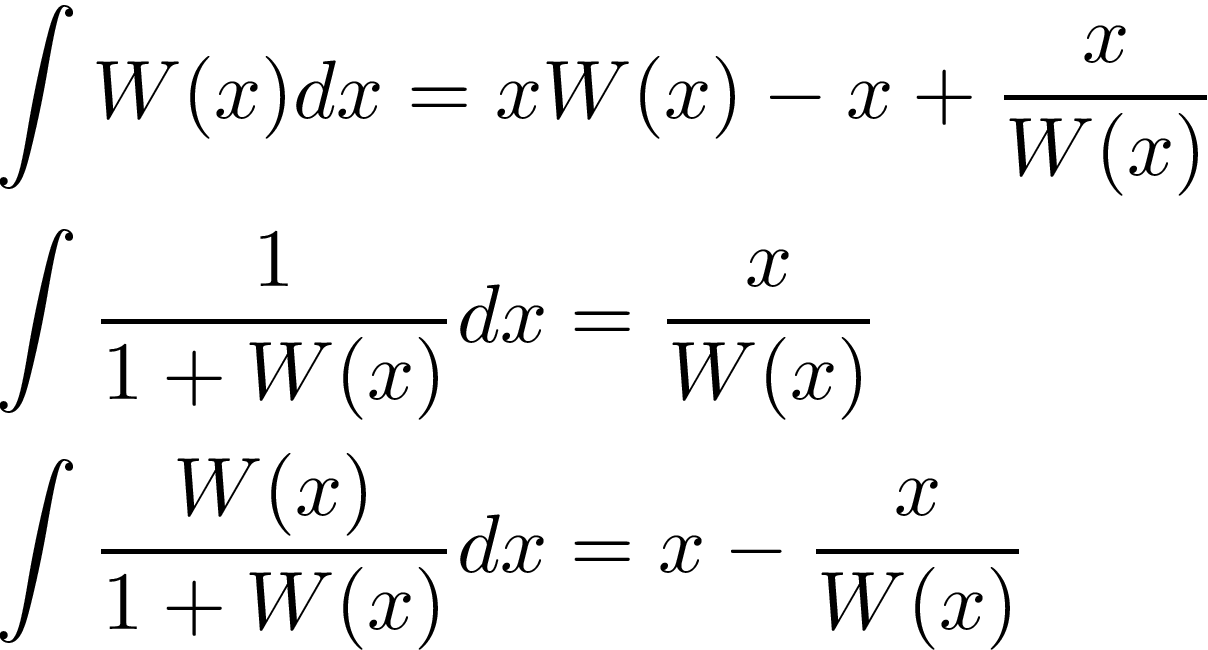
The Lambert function can be used in order to solve some transcendental equations. For example, consider the equation:
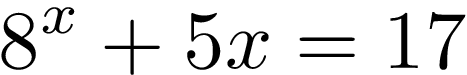
We can proceed as follows:
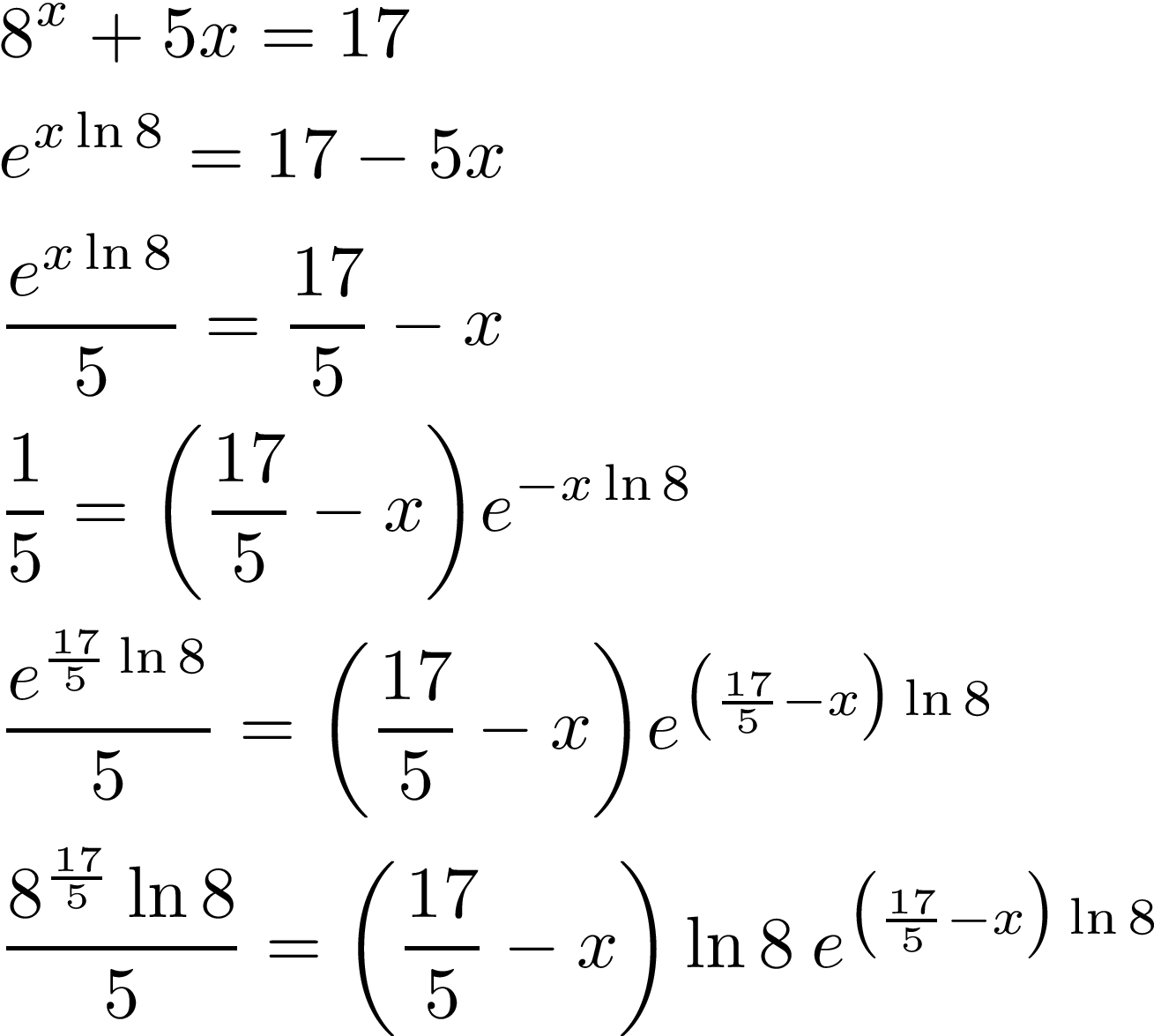
We can make the following change of variable:
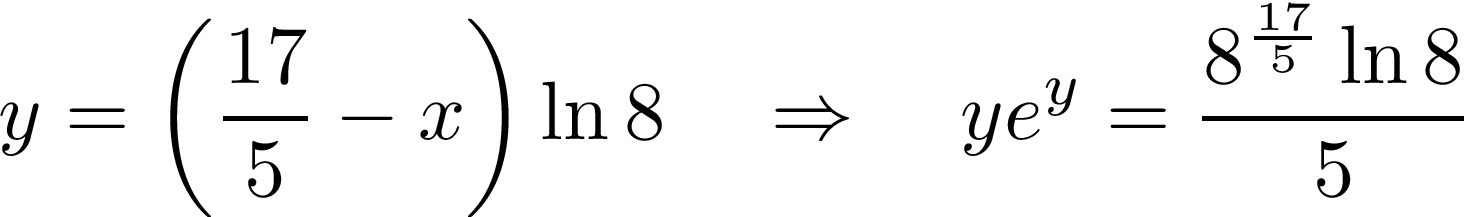
This implies:
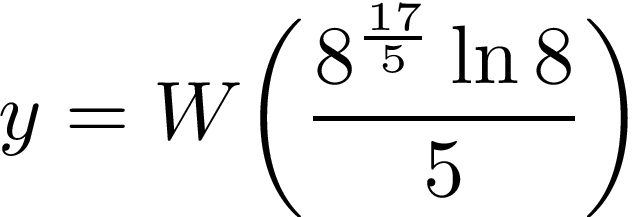
Finally, inverting the change of variable, we conclude:
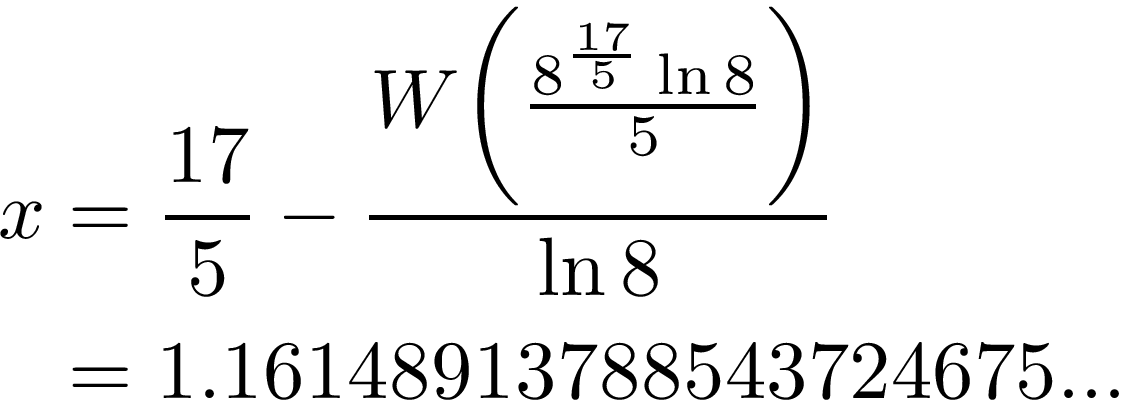
Not sure you want to subscribe? Take a peek at the description of the Blue Moonshine channel to get an idea of its contents.